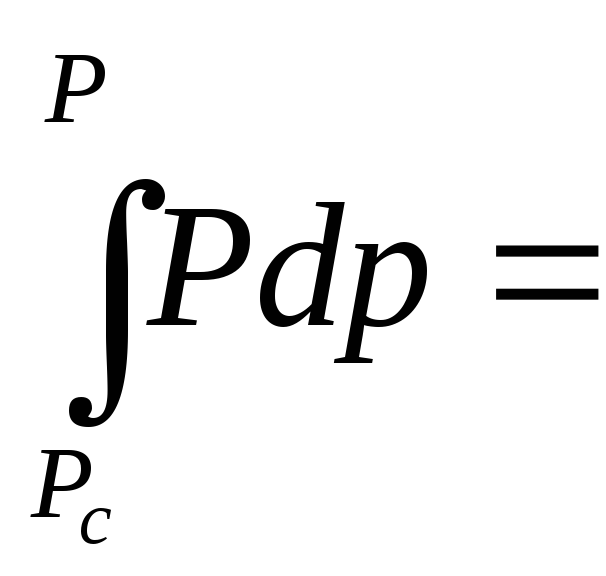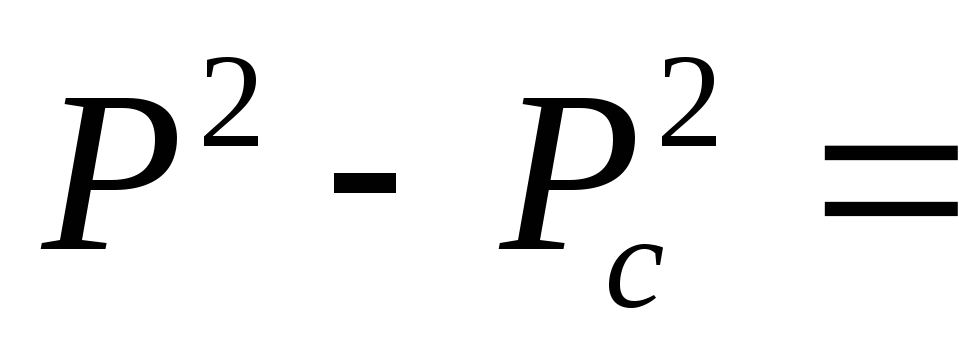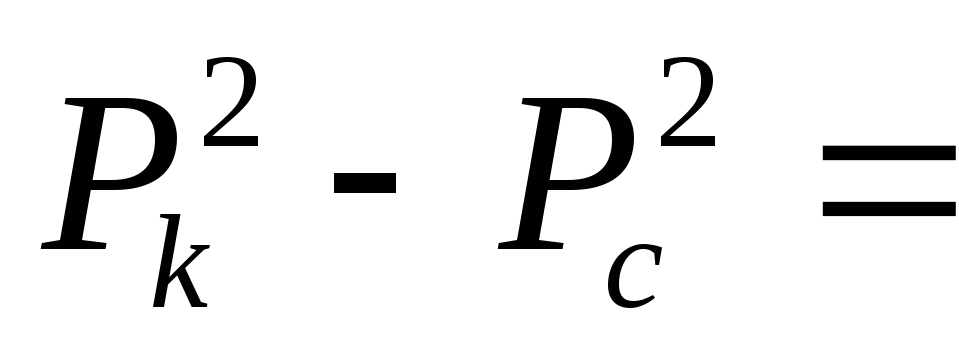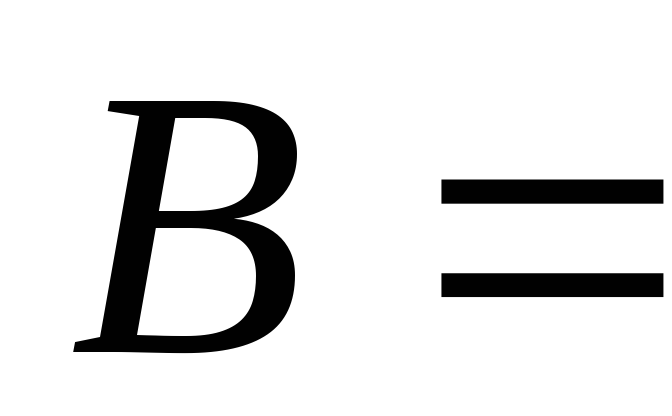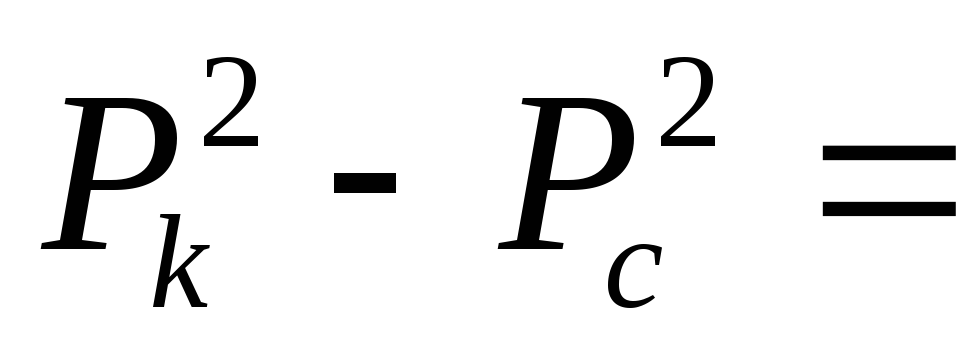Воронка депрессии уравнение распределения по пласту плоскорадиальный поток

1.6. Плоскорадиальная фильтрация несжимаемой жидкости

Распределение давления и скорости фильтрации в пласте при плоскорадиальной установившейся фильтрации происходит в соответствии с выражением величины дебита (объемного расхода) скважины, называемого формулой Дюпюи, по имени ее автора — французского инженера гидравлика XIX века:

, (1.5)

где k – проницаемость,

h – эффективная насыщенная толщина пласта,

μ – вязкость фильтруемой жидкости,

p_K – пластовое давление на контуре питания,

p_C – пластовое давление в призабойной зоне,

R_K – радиус контура питания,

r_C – радиус скважины,

Круговой пласт толщиной h и радиуса R_К (см. рис. 3) вскрывает центральная скважина радиуса r_С, на забое которой поддерживается постоянное давление p_C. На боковой поверхности также поддерживается постоянное давление p_K (p_К>p_С), и через нее происходит приток флюида, равный дебиту скважины.

Рис. 3. Плоскорадиальный поток

в круговом пласте

Боковая поверхность, через которую происходит приток, называется контуром питания. Давление в пласте распределено по логарифмическому закону. Поэтому при значениях радиуса, близких к радиусу контура питания, значения давления изменяются незначительно, но при приближении к скважине давление изменяется резко. Поверхность, которые получаются вращением логарифмической кривой вокруг оси симметрии скважины, соответствует распределению давления и носит название воронки депрессии (рис. 4).

Аналогично ведет себя и градиент давления, а, следовательно, и скорость фильтрации (с той лишь разницей, что давление при приближении к скважине резко уменьшается, а скорость резко возрастает).

Из физических соображений подобное поведение функций, определяющих изменение в пласте давления и скорости фильтрации, легко объяснимо. В самом деле, через любую цилиндрическую поверхность, концентрично расположенную относительно скважины, в единицу времени протекает один и тот же объем несжимаемой жидкости (Q = const). Поскольку вблизи контура питания площадь боковой поверхности цилиндра очень велика, скорости там малы. При приближении к скважине площадь поверхности постоянно уменьшается, а скорость возрастает.

Рис. 4. Распределение давления

в плоскорадиальном потоке

2. Задание для выполнения лабораторной работы

Основываясь на результатах лабораторных исследований керна по скважине, определить значение проницаемости и прогнозные значения дебита нефти, дебита жидкости и обводненности скважины в динамике (в зависимости от величины отбора от НИЗ).

Ответы предоставить в виде значения проницаемости, графика кривых ОФП, графика кривых изменения давлений и графика технологических показателей работы скважин (дебита нефти, дебита жидкости, обводненности) в координатах «дебит (обводненность) – отбор от НИЗ».

В расчетах принять следующие параметры:

— вязкости нефти и воды принять равными µ = 10 мПа*с;

— эффективную нефтенасыщенную толщину принять равной 8 м;

— радиус контура питания R_К = 500 м;

— радиус скважины r_С = 0.1 м;

— скин-фактор (как эффект от ГРП) = -4 ед.;

— значение начальной водонасыщенности пласта принять равным 0.25, 100% отбору от НИЗ соответствует значение водонасыщенности пласта, при котором фазовая проницаемость по нефти становится равной 0.

Данные для работы предоставлены в виде табличных и графических приложений П.1-П.6.

Источник

Плоскорадиальный поток идеального газа по двучленному закону фильтрации

Вблизи высокодебитных газовых скважин происходит нарушение закона Дарси, поэтому все гидродинамические расчеты строятся на основе двучленного закона фильтрации (5.10). При этом нельзя использовать диф. уравнение (6.9), т.к. оно получено с учетом уравнений движения по закону Дарси (6.2). Поэтому будем интегрировать уравнение (5.10), считая фильтрацию плоскорадиальной:

; где ,,

. (5.10)

Найдем распределение давления Р(r) в круговом пласте и выведем формулу притока газа к скважине.

Выразим скорость фильтрации через приведенный объемный дебит , используя формулу (2.14) для плотности(Р) и соотношение.

. (6.31)

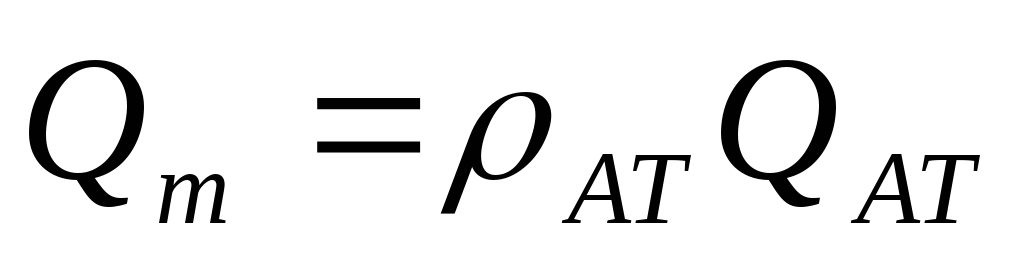
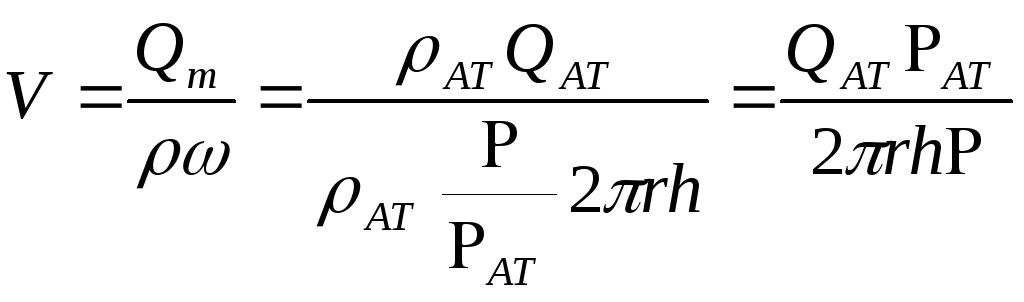
Подставим выражение (6.31) в (5.10) с учетом выражения (2.14) для (Р), получаем:

.

(*)

и проинтегрируем от забоя скважины (P=P_c; r=r_c) до произвольной точки пласта (P;r):

.

В результате будем иметь

, (6.32)

. (6.33)

Распределение давления по формуле (6.33) отличается от распределения давления по формуле (6.26) ( при сохранении закона Дарси) наличием последнего слагаемого.

Проинтегрируем уравнение (*) от забоя (P=P_c; r=r_c) до контура питания (P=P_k; r=r_k) и пренебрегая 1/R_k по сравнению с 1/r_c , получим уравнение притока газа к скважине.

(6.34)

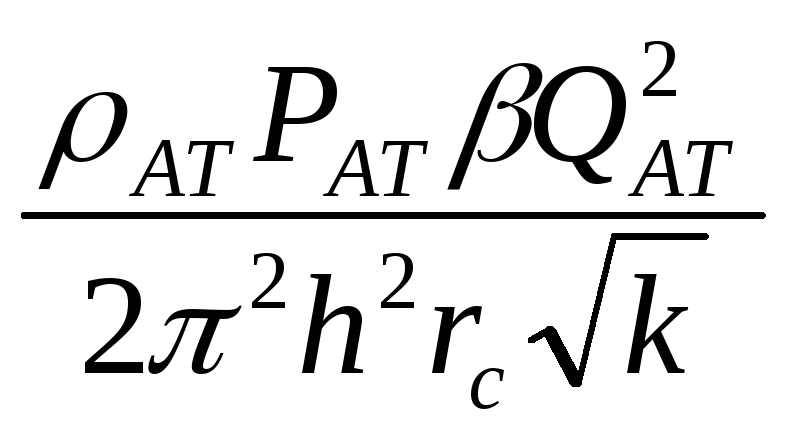
Обычно вводят обозначения:

;

; (6.35)

тогда уравнение (6.34) принимает вид:

. (6.36)

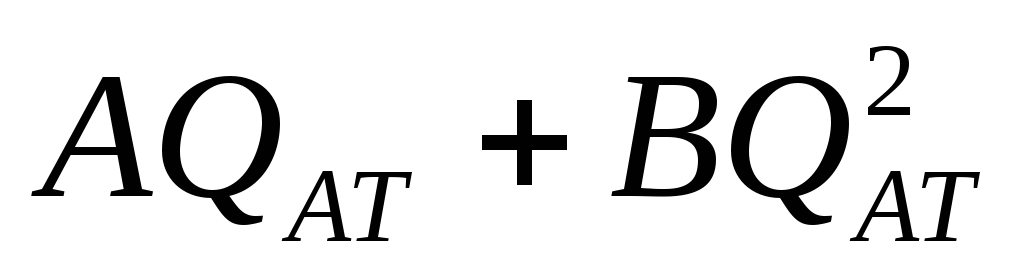
Коэффициенты фильтрационных сопротивлений А и B определяют опытным путем по данным исследования скважин при установившихся режимах.

Газовая скважина исследуется на 5-6 режимах; на каждом режиме измеряется дебит и определяется забойное давление (по устьевому давлению). Затем скважину закрывают и давление в остановленной скважине принимают за контурное давление P_k.

После этого можно найти (вычислить) значение коэф. А и В по индикаторной линии, построенной по уравнению (6.36) , которая представляет собой параболу выпуклостью к оси дебитов (рис.40).

Однако удобнее уравнение (6.36) записать в виде :

. (6.37)

График уравнения (6.37) , построенный в координатах Q_АТ и , представляет собой прямую, у которой А- отрезок на оси ординат; а В =, -угол наклона прямой к оси абсцисс. (рис.41)

Рис. 40 Рис. 41

Уравнение притока (6.36) газа к скважине широко используется в расчетах при проектировании разработки газовых месторождений. Кроме того, по найденному значению А (путем исследования скважины) можно определить коллекторские свойства пласта, например, коэффициент гидропроводности

. (6.38)

7. Плоскорадиальный фильтрационный поток реального газа по закону Дарси

Если пластовое давление выше 10Мпа и депрессия не слишком мала (P/P_k 0.9) , то уравнение состояния газа значительно отклоняется от уравнения состояния идеального газа и плотность определяется по формуле (2.16)

, (2.16)

т.е. .

Кроме того, для высоких пластовых давлений нужно учитывать зависимость вязкости от давления, которая определяется выражениями (2.21) или (2.22)

;

;

или по графикам ; проницаемость при этом будем считать постоянной (k=сonst).

Если фильтрация установившаяся и выполняется закон Дарси, то справедливо уравнение (6.9) , в котором под функцией Лейбензона надо понимать выражение (6.4) , т.е.

++(6.9)

. (6.4)

Для реального газа выражение (6.4) с учетом (2.16) имеет вид:

. (6.39)

Найдем дебит скважины при плоскорадиальном движении. Используя аналогично методу установившейся фильтрации несжимаемой жидкости и газа, напишем выражение для дебита , заменяя в ф-ле Дюпюи объемный дебит массовым, а KP/— значениями функции Лейбензона (6.39):

(6.40)

Переходим к дебиту , приведенному к атмосферному давлению

. (6.41)

Вычисление интеграла в (6.41) можно произвести приближенно: по графикам зависимости Z(P) и (P) определяются значения Z(P_c)=Z_c; Z(P_k)=Z_k и ,;значенияиZ(P) в (6.41) заменяются постоянными значениями, равными средним значениям ;.

Тогда интеграл в (6.41) вычисляется аналитически и формула (6.41) принимает вид

. (6.42)

Как видим выражение (6.42) определяющее дебит реального газа отличается от выражения (6.28) для дебита идеального газа множителем в знаменателе и среднепластовым значением вязкости.

Источник