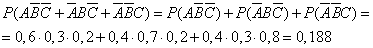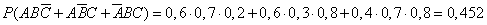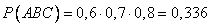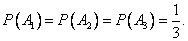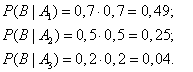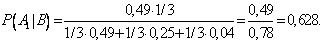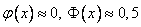Только радости по теории вероятности

После радости неприятности по теории вероятности

Конец второй декады октября. Погода — просто не нарадуюсь!
Гуляла не спеша по городу, подмечая каждый штрих осени. Меня умиляли шелест пёстрой листвы и пьянящее дыхание тёплого ветра, прилетевшего с берегов Балтийского моря.
Небо манило и ревниво «требовало: «Обними меня!» И я, любуясь лазурным куполом, делала это снова и снова.

Фотоаппарат «веселился» вместе со мной и «поглощал» кадр за кадром: кусты пурпурно- бордовых роз, мётлы сиреневых, розовых, фиолетовых сентябринок, розовых хризантем, шикарное поле ромашек и золотом осыпанные деревья. Невозможно оторваться! Красота! В душе звенела музыка.
Я напевала:

Листья жёлтые над городом кружатся,
С тихим шорохом нам под ноги ложатся.
И от осени не спрятаться, не скрыться,
Листья жёлтые, скажите, что вам снится?

Зайдя в подъезд, обнаружила — лифт не работает! «Мой бог! Восьмой или девятый раз за месяц?» — негодовала я, начиная подниматься на девятый этаж.
В подъезд зашла пара средних лет. Тоже начали что- то бурчать по поводу лифта. Я успокоилась и, неожиданно для себя, уверенно произнесла:
— Всё же лучше пешком пять минут, чем стоять в лифте тридцать пять в ожидании монтёра. Три дня назад я потеряла это время в «засаде» на втором этаже. А моему внуку и зятю повезло больше, жильцы на другом этаже вызвали лифт и он стал подниматься выше.
Парочка притихла. А у меня в голове закрутились слова из песни: «После радости неприятности по теории вероятности». С ними я вошла в квартиру.

«Уничтожив» лёгкий ужин, села за компьютер. И песня перестала преследовать меня.

Я «пробежалась» по страницам в «Контакте» и «Одноклассниках».
С радостью ответила на сообщения друзей. Посмотрела новости в группах.

«Теперь можно и на «прозушку» заглянуть! Меня интересовала информация по поводу предстоящего Конкурса- 6. Может, она порадует выбранной темой и началом конкурса?»- подумала и,окрылённая последней мыслью, открыла сайт.
Лучше бы не думала.

Для испытания мне была уготовлена другая новость, «сразившая» наповал радость ожидания:
«Конкурс- 6. Выбор темы. Мониторинг»!

Нужно было выбрать три из десяти тем до десятого ноября.
Ещё три недели томиться.
Всё же, смирившись с новостью, выбрала: один, четыре, девять.
Из-за минутного расстройства выпустила тему под номером девять, написав в рецензии только «один» и «четыре»!
Следом за «рецкой», как говорится, «не отходя от кассы», хотела написать сообщение одному из авторов сайта. У него на странице кликнула на «личное сообщение». Опаньки! Сервер исчез!

Совпадение или «после радости неприятности. »? Подозрительно! Однако, я удивилась, даже запаниковала чуть-чуть. Что за наваждение такое, что это значит? Ирония судьбы, не иначе! Не написать, не позвонить, хоть плачь! А ведь такой чудесный день был.

Снилось мне море из моих слёз. Тонула я и выплывала, и снова тонула и выплывала. Ни души рядом!
Лишь на один миг корабль показался в морской дымке и тут же исчез. И откуда чуть слышно доносилось трио Вадима Мулермана, Владимира Шаинского и Юрия Энтина: «В нашей жизни, как в природе чередуется окраска, если хвалят вас сегодня, значит завтра будет встряска. ».

Проснулась помятая, как солёный огурец! «Просолилась слезами»,- смеясь над собой, подумала я.
Гимнастика. Умылась. Лёгкий завтрак.
И маета! Как я жила раньше без «прозушки»?

Целые сутки провела в ожидании, будто навек с любимой подружкой рассталась.
При очередном поиске связи волновалась, как на первом свидании. А сайт выдавал: «Сервер не найден»!
А в голове по-предательски выстукивала мелодия и крутились слова:

«Столько песен, счастья столько,
что живу друзья в надежде.
Будут радости и только,
а пока идут как как прежде после радости
неприятности по теории вероятности. ».

. Время от времени прекрасный человек волновался за меня и писал смс в Контакте:
— Лида, привет! Сижу на остановке автобуса. Еду до метро. «Проза»включилась?

Как мило с её стороны:

— Лида, привет! Я дома у компа, «Проза» и «Стихи» работают. Пошла в магазин за продуктами.

Удивительный человек! Великодушный! Сердечный! Ей надо в магазин сходить, по дому управиться, а она нашла таки минутку- другую для участия и поддержки!
Бесценная моя, если б ты знала, как я ценю и дорожу нашей дружбой!

Источник

Теория вероятностей, формулы и примеры

О чем эта статья:

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Дискретная случайная величина — величина, которая в результате испытания может принимать определенные значения с определенной вероятностью, то есть образовывать счетное множество.

Элементы множества можно пронумеровать. Они могут быть как конечными, так и бесконечными. Например: количество выстрелов до первого попадания в цель.

Непрерывная случайная величина — это такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка. Количество возможных значений непрерывной случайной величины бесконечно.

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Вероятностное пространство — это тройка (Ω, Σ, Ρ) иногда обрамленная угловыми скобками: ⟨ , ⟩ , где

• Ω — это множество объектов, которые называют элементарными событиями, исходами или точками.
• Σ — сигма-алгебра подмножеств , называемых случайными событиями;
• Ρ — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что .

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

• Вероятность достоверного события равна единице.
• Вероятность невозможного события равна нулю.
• Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

• 0 ≤ P(A) ≤ 1.

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

1. A — встреча с другом состоится, х и у — время прихода. Значит:
   0 ≤ х, у ≤ 60.
2. В прямоугольной системе координат этому условию удовлетворяют точки, которые лежат внутри квадрата ОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то есть:

x−y y.

Этим неравенствам удовлетворяют точки из области G — то, что выделено красным:

Тогда вероятность встречи равна отношению площадей области G и квадрата:

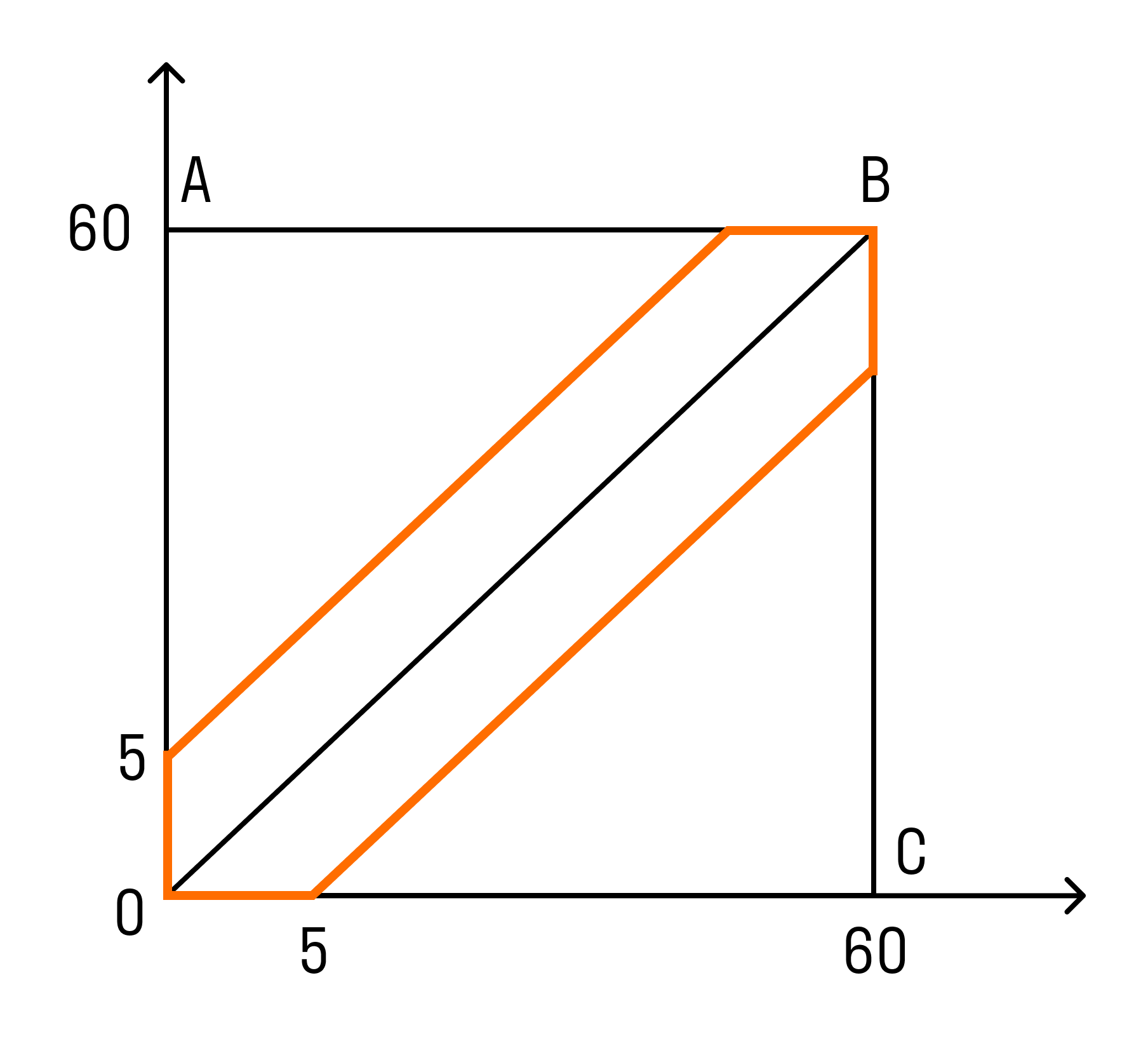
P(A)=S_G/S_OABC= 60 * 60 — 55 * 5560 * 60 = 23144 = 0,16

У нас есть отличное онлайн обучение по математике для учеников с 1 по 11 классы, записывайся на пробное занятие!

Сложение и умножение вероятностей

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

• P(A₁) + P(A₂) + … + P(A_n) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1. 
2. 
3. 

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

Если событие А может произойти только при выполнении одного из событий B₁, B₂, . B_n, которые образуют полную группу несовместных событий — вероятность события А вычисляется по формуле полной вероятности:

Вновь рассмотрим полную группу несовместных событий B₁, B₂, . B_n, вероятности появления которых P(B₁), P(B₂), . P(B_n). Событие А может произойти только вместе с каким-либо из событий B₁, B₂, . B_n, которые называются гипотезами. Тогда по формуле полной вероятности: если событие А произошло — это может изменить вероятности гипотез P(B₁), P(B₂), . P(B_n).

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

1. Возможны три гипотезы:
   • А1 — на линию огня вызван первый стрелок,
   • А2 — на линию огня вызван второй стрелок,
   • А3 — на линию огня вызван третий стрелок.

2. Так как вызов на линию огня любого стрелка равно возможен, то
   
3. В результате опыта наблюдалось событие В — после произведенных выстрелов мишень не поражена. Условные вероятности этого события при наших гипотезах равны:
   
4. По формуле Байеса находим вероятность гипотезы А₁ после опыта:
   

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

• Бросаем игральный кубик, где вероятности выпадения определенной цифры одинаковы в каждом броске.
• Включаем лампы с заранее заданной одинаковой вероятностью выхода из строя каждой.
• Лучник повторяет выстрелы по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой.

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Обозначим вероятность появления события А в единичном испытании буквой р, значит:

p = P(A), а вероятность противоположного события (событие А не наступило) — буквой q

q = P(¯A) = 1 — p.

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли:

P_n(k) = C_n k * p k * q n-k , где q = 1 — p.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

np — q ≤ k ≤ np + p, где q=1−p

Так как np−q = np + p−1, то эти границы отличаются на 1. Поэтому k, являющееся целым числом, может принимать либо одно значение, когда np целое число (k = np), то есть когда np + p (а отсюда и np — q) нецелое число, либо два значения, когда np — q целое число.

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

1. По условию дано: n = 730, p = 1/365, g = 364/365
2. np — g = 366/365
3. np + p = 731/365
4. 366/365 ≤ m ≤ 731/365
5. m = 2

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

1. По условию дано: n = 1000, p = 0,002, λ = np = 2, k = 3.
2. Искомая вероятность после подстановки в формулу:

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Пусть в каждом из n независимых испытаний событие A может произойти с вероятностью p, q = 1 — p (условия схемы Бернулли). Обозначим как и раньше, через P_n(k) вероятность ровно k появлений события А в n испытаниях.

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

• 
• при больших x верно

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник

Читайте также:  Симптомы чувство тяжести внизу живота