Коэффициент депрессии дробового шума

Случайные величины возникают при рассмотрении «выборок» случайных процессов, т. е. значений различных случайных функций времени в дискретные моменты. При этом нормальными, или гауссовыми, случайными процессами называются такие процессы, выборки из которых имеют распределение Гаусса (см. § 59), или, что то же самое, характеристическую функцию вида (58.07).

В теории оптимальных приемников обычно предполагают, что помеха является стационарным случайным процессом нормального типа. Часто делают еще одно дополнительное предположение (от которого мы полностью освободились в данной книге), что помеха является «белым шумом», т. е. имеет постоянную спектральную интенсивность, и, будучи некоррелированной во времени («абсолютно случайный процесс»), может быть представлена, как беспорядочное наложение возмущений с нулевой длительностью (ср. § 12 и 17). Существенно отметить, что собственные шумы приемника — тепловые и дробовые, которые будут подробно рассмотрены ниже, дают основание для такой идеализации. Однако представление о

помехе как о белом шуме ведет к Некоторым математическим трудностям, не вполне соответствует физической реальности и, что особенно важно, не позволяет включить в рассмотрение интересный вид помех, встречающихся в радиолокации, а именно помех, обусловленных хаотическими отражениями (см. гл. XI).

Поскольку внутренние шумы приемников рассматриваются на протяжении всей книги, целесообразно разобрать вкратце физическую сторону этих явлений.

Тепловые шумы возникают вследствие теплового движения электрических зарядов в проводниках. В каждом сопротивлении, находящемся при абсолютной температуре в состоянии термодинамического равновесия, в результате флюктуаций возникает случайная электродвижущая сила спектральная интенсивность которой равна

где постоянная Больцмана, сопротивление. Это соотношение применимо к любому элементу электрической цепи, причем в общем случае определяется по формуле

где импеданс данного элемента при частоте со.

Мы видим, что для чисто омического сопротивления, не зависящего от частоты, флюктуационная электродвижущая сила является белым шумом, поскольку ее спектральная интенсивность является константой. Фактически, разумеется, при достаточно высоких частотах постоянство всегда нарушается вследствие остаточных емкостей или индуктивностей, скин-эффекта или квантовых явлений. Нужно еще учесть, что при росте частоты квазистационарное рассмотрение цепи и вместе с ним формула (61.01) теряют свой смысл.

Оказывается, что для металлических проводников формулу (61.01) можно применять в случае, когда по ним текут постоянные или переменные токи, т. е. когда, строго говоря, термодинамическое равновесие отсутствует. Объясняется это тем, что прохождение не слишком сильных токов через металлический проводник возмущает тепловое движение электрических зарядов лишь в незначительной степени, так что флюктуации по-прежнему, подчиняются формуле (61.01).

Дробовой эффект в электронных лампах возникает как результат дискретной структуры электронного потока.

Если, например, мы имеем диод, к которому приложено достаточно большое анодное напряжение, так что все испускаемые катодом электроны поступают на анод (рис. 56, а), то вследствие флюктуаций катодной эмиссии на средний анодный ток накладывается случайный «дробовой» ток со спектральной интенсивностью

где есть абсолютная величина заряда электрона. Мы видим, что возникающий благодаря дробовому эффекту, также можно считать белым шумом, поскольку его спектральная интенсивность не зависит от .

Рис. 56. Электронные потоки в диоде: а) обычный диод—электроны движутся от катода к аноду; б) «равновесный» диод—электроны движутся навстречу друг другу и полный анодный ток равен нулю.

Фактически, если под понимать то к во внешней цепи диода, формула (61.03) применима при условии

где есть время пролета электрона через диод или длительность импульса во внешней цепи, появляющегося при прохождении одного электрона от катода к аноду. При происходит резкое спадание спектральной интенсивности дробовых шумов.

В сущности говоря, дробовой шум является физической реализацией той модели случайного процесса, которую мы рассматривали в § 12, поскольку он состоит из беспорядочно возникающих возмущений (импульсов) стандартной формы.

Благодаря наличию пространственного заряда в электронных лампах лишь часть испускаемых катодом электронов доходит до анода. Оказывается, что пространственный заряд уменьшает дробовой эффект, так что для диода формула (61.03) видоизменяется следующим образом:

где есть так называемый коэффициент депрессии дробового эффекта, -анодный ток.

Отметим, что электронная лампа является

неравновесной системой, поэтому для нее формула (61.01) неприменима и флюктуации имеют совершенно иную физическую природу, что и находит свое отражение формулах (61.03) и (61.05) для диода. Интересно, что можно себе представить электрическую цепь с «равновесным» диодом (рис. 56, б), катод и анод которого находятся при одинаковых температуре и напряжении и выполнены из одного и того же материала, способного испускать электроны. Если для простоты считать, что по внешней цепи анод и катод замкнуты накоротко, и обозначить через внутреннее сопротивление равновесного диода (по отношению к малым анодным напряжениям и токам), то тепловая возникающая в равновесном диоде, будет связана с флюктуационным током через диод соотношением

поэтому по формуле (61.01) получаем

С другой стороны, при не слишком больших плотностях заряда соударениями электронов друг с другом в пространстве между катодом и анодом можно обычно пренебречь, поэтому единственным «случайным элементом» в системе, изображенной на рис. 56, б, является электронная эмиссия. Если обозначить через ток, который проходит от катода к аноду, то ток в равновесном диоде будет течь в противоположном направлении от анода к катоду, причем каждый из этих токов должен испытывать дробовой эффект. Поэтому для равновесного диода мы должны иметь формулу

Формулы (61.07) и (61.08) должны совпадать, поэтому сопротивление равновесного диода должно быть равно

Детальное микроскопическое рассмотрение электронных потоков в диоде подтверждает последнее выражение. Таким образом, в данном примере дробовой и тепловой шумы представляют собой разные названия для одного и того же явления.

При отсутствии теплового равновесия спектральную интенсивность дробового тока часто представляют в виде

где называется коэффициентом депрессии тепловых шумов. Оказывается, что в диоде с задерживающим напряжением и холодным анодом

причем в этом случае формулы (61.03) и (61.10) эквивалентны. В плоском диоде с ускоряющим анодным напряжением и сильным пространственным зарядом (таким, что справедлив так называемый закон трех вторых, по которому анодный ток в основном определяется анодным напряжением и практически не зависит от тока эмиссии)

причем в этом случае коэффициент в формуле (61.05) мал.

Выше мы рассмотрели простейшие системы, в которых проявляются тепловые и дробовые шумы. В реальных системах эти шумы подвергаются преобразованиям. Например, в приемных устройствах дробовой и тепловой эффекты усиливаются, претерпевают фильтрацию и т. д. В теории оптимальных приемников мы предполагаем, что помеха, эквивалентная всем внутренним шумам приемника, как бы отнесена к его входному звену и представлена в виде случайного процесса с известными статистическими свойствами.

Тепловые и дробовые шумы являются классическими примерами нормальных случайных процессов, причем после прохождения через линейные системы (частотные фильтры) они остаются нормальными. Последнее следует просто из того, что при линейном преобразовании

новые случайные величины по-прежнему являются нормальными, т. е. имеют распределение Гаусса.

Другим примером нормального Случайного процесса, как мы уже указывали, является радиолокационная помеха, вызванная отражением., от многих хаотически движущихся рассеивателей (см. гл. XI).

Источник

Оптимизация шумовых параметров сигнальных цепей. Часть 1

Эта статья посвящена обеспечению требуемых шумовых параметров цепей обработки сигналов. Мы рассмотрим характеристики шумов в полупроводниках. Эти виды шума присущи всем интегральным схемам. В статье объясняется, как шум специфицируется в технической документации на полупроводниковые приборы, и показано, каким образом можно оценить шумовые характеристики источника опорного напряжения (ИОН) в реальных условиях эксплуатации, не приведенных в документации.

Сегодня понимание природы и свойств электрического шума важно, как никогда прежде. Когда 14- и 16-разрядные преобразователи становятся обыденностью, а 18- и 24-разрядные преобразователи все доступнее, шум часто оказывается единственным фактором, ограничивающим системные характеристики. Очевидно, что понимание причин возникновения и характеристик шумов в интегральных схемах — это ключ к достижению наивысшей точности системы.

Шум может вывести из себя кого угодно, но особенно он раздражает разработчиков аналоговых приборов. Вообще говоря, шум — совершенно нежелательное электрическое явление в любой цепи обработки сигналов. В зависимости от происхождения, шум можно классифицировать как внешний (интерференция, помеха) или внутренний (внутренне присущий, неотъемлемый). Это проиллюстрировано блок-схемой канала обработки сигнала (рисунок 1). Здесь все внутренние источники шума (Vint) объединены на выходе, а все внешние источники шума (Vext) — на входе сигнальной цепи.

Рис. 1. Шум в сигнальной цепи

Разработчику важно понимать причины возникновения внутреннего шума в полупроводниках и его характеристики. В зависимости от причины возникновения выделяют следующие типы внутреннего шума: тепловой, дробовой, фликкер-шум, шум лавинного умножения и шум, вызванный случайными скачками тока, а также шумы, специфичные для преобразователей данных: шум дискретизации, дрожание апертуры и гармонические искажения. Разработчик должен также знать, можно ли предотвратить появление шумов того или иного типа, или они неизбежны.

Шумы в полупроводниковых устройствах

Генерация шума свойственна всем электрическим компонентам, в том числе – всем полупроводниковым приборам и резисторам. Мы начнем с обсуждения общих свойств шума, а затем рассмотрим типы и характеристики общепринятых источников шума. Далее мы научимся находить в технической документации шумовые параметры и интерпретировать их. В завершение используем всю эту информацию для расчета выходного шума источника опорного напряжения, работающего в условиях, не определенных в технической документации.

Свойства шума

Следующий раздел посвящен описанию природы шума в полупроводниках и тому, как определяют шум в полупроводниковых устройствах.

Амплитуда шума

Первопричиной всех шумов в полупроводниках являются случайные процессы, поэтому предсказать величину мгновенной амплитуды шума невозможно. Амплитуда описывается гауссовским (нормальным) распределением. Обратите внимание, что среднеквадратичное (RMS) значение шума (Vn) представляет собой стандартное отклонение (σ) распределения шума. Среднеквадратичное и пиковое напряжения источника случайного шума связаны между собой соотношением:

Для любого сигнала отношение величины полного размаха (peak-to-peak) напряжения к его среднеквадратичному значению (V_{nP_P}/V_nRMS) называют пик-фактором (crest factor) или коэффициентом амплитуды. В данном уравнении коэффициент 6,6 — обычно используемый пик-фактор. Это значение обусловлено тем, что статистически на выходе гауссова источника шума напряжение, полный размах которого в 6,6 раза превышает среднеквадратичное, присутствует в течение 0,01% полного временного интервала наблюдения. Это затененная область под графиком плотности шумового напряжения, приведенного на рисунке 2. Вероятность того, что амплитуда напряжения выйдет за указанные границы ±3σ, равна 0,0001. Важно помнить, что коррелированные сигналы суммируются линейно, тогда как случайные сигналы (такие как шумы) складываются геометрически, то есть как квадратный корень из суммы квадратов.

Рис. 2. Гауссовское распределение шума

Спектральная плотность шума

Источники шума в полупроводниках по виду графиков, отражающих их спектральную плотность, можно разделить на две категории. На высоких частотах доминирует белый шум, а на низких — розовый шум. Для белого шума характерна равномерная спектральная плотность (рисунок 3). В этом случае энергия сигнала будет одинакова в любой заданной полосе частот. В случае розового шума энергия сигнала будет одинакова в каждой декаде. Он характеризуется спектральной плотностью (рисунок 4), которая обратно пропорциональна частоте, из-за чего розовый шум часто называют 1/f-шумом.

Рис. 3. Спектральная плотность белого шума

Рис. 4. Спектральная плотность розового шума

На рисунке 4 Kv — константа, соответствующая экстраполированному значению en при f = 1 Гц. Обе оси координат на рисунке приведены в логарифмическом масштабе.

Шум, обнаруживаемый в полупроводниковых приборах, является комбинацией белого и розового шумов, что в результате дает спектральную плотность, график которой приведен на рисунке 5. Оси координат здесь также имеют логарифмический масштаб. Частота излома (FC) — граница между розовым и белым шумом.

Рис. 5. Спектральная плотность шума

Напряжение шума в полосе частот определяется площадью под кривой спектральной плотности шума между верхней (Fh) и нижней (Fl) частотами полосы. Математически это записывается в виде:

где ND — спектральная плотность шума; Fc — частота излома; Fl — нижняя граница полосы частот; Fh — верхняя граница полосы частот. упрощая, получаем:

Как можно видеть, амплитудное значение шума должно всегда даваться в частотном диапазоне.

Виды шума в полупроводниках

Как уже говорилось, источники шума в полупроводниках можно отнести к одной из двух категорий в зависимости от формы кривой, описывающей их спектральную плотность. Эти две категории — белый и розовый шумы. Рассмотрим подробнее каждый тип шума.

Белый Шум

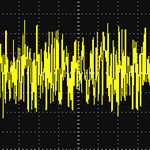
Рис. 6. Осциллограмма белого шума (1 мкс/дел.)

Для белого шума характерна равномерная спектральная плотность с одинаковой энергией шумового сигнала в любой заданной полосе частот. Название для такого типа шума пришло из оптики, где свет с одинаковой амплитудой во всем спектре имеет белый цвет. Осциллограмма белого шума имеет характерный вид, показанный на рисунке 6. В полупроводниковых приборах выделяют три источника белого шума: тепловой, дробовой и лавинный.

Тепловой шум. Тепловой шум, также называемый шумом Джонсона, генерируется всеми пассивными резистивными элементами. Причина его появления — случайное броуновское движение электронов в резистивной среде. Тепловой шум увеличивается с ростом температуры и сопротивления и часто оказывается самой существенной составляющей шума в прецизионных полупроводниковых преобразователях данных.

Все пассивные резистивные элементы – как дискретные, так и интегральные, – генерируют тепловой шум. Наличие постоянного тока не оказывает влияния на уровень теплового шума, но он увеличивается с ростом температуры и сопротивления. Резисторы, даже изолированные, всегда генерируют шум.

Плотность теплового шума (ND — Noise Density) определяется следующим образом:

где k — постоянная Больцмана, R — сопротивление в [Ом], а T — температура в [K].

Дробовой шум. Дробовой шум, также называемый шумом Шоттки, генерируется в активных приборах, когда заряд проходит через потенциальный барьер. Потенциальные барьеры имеются в транзисторах и диодах. Дробовой шум генерируется из-за того, что поток зарядов, проходящих через переход, не является непрерывным. Он формируется отдельными электронами, время прихода которых — случайная величина. Постоянный ток, который мы видим на макроскопическом уровне, в действительности представляет собой сумму множества случайных микроскопических импульсов тока. Именно случайные вариации тока обеспечивают дробовому шуму гауссовскую равномерную спектральную плотность (белый шум). Уровень дробового шума увеличивается с ростом тока.

Плотность дробового шума определяется следующим образом:

где q — электрический заряд, а I — протекающий через барьер ток.

Лавинный шум (шум лавинного умножения). Источниками лавинного шума являются PN-переходы, работающие в режиме обратного пробоя, как это происходит в стабилитронах (зенеровских диодах). Ток, генерируемый во время лавинного пробоя, состоит из случайно распределенных шумовых выбросов, проходящих через обратно-смещенный переход. Как и в случае дробового шума, для генерации лавинного шума требуется наличие тока, но обычно он гораздо интенсивнее.

Розовый шум

Розовый шум характеризуется спектральной плотностью, растущей по мере уменьшения частоты. В данном случае энергия сигнала одинакова в каждой частотной декаде. Это создает спектральную плотность мощности, обратно пропорциональную частоте. Название для такого типа шума также пришло из оптики, где свет, в спектре которого доминируют низкочастотные составляющие, имеет розовый цвет. Розовый шум присущ всем активным и некоторым пассивным приборам.

В полупроводниковых приборах различают две разновидности розового шума — фликкер-шум (flicker noise) и шум, вызванный случайными скачками тока (popcorn noise).

Рис. 7. Вид осциллограммы фликкер-шума
(1 с/дел.,полоса частот 0,1…10 Гц)

Фликкер-шум. Фликкер-шум (также называемый 1/f-шумом или контактным шумом) — избыточный шум, генерируемый случайными флуктуациями тока, причиной которых являются дефекты в полупроводниковых материалах. Такой шум присущ транзисторам всех типов и некоторым типам резисторов. Фликкер-шум генерируют диффузионные резисторы и композитные угольные резисторы, поскольку они выполнены из полупроводниковых материалов. Фликкер-шум тесно связан с постоянным током.

Плотность фликкер-шума определяется следующим образом:

где K — константа, определяемая прибором, I — постоянный ток, а f — частота.

Механизмы возникновения фликкер-шума могут быть самыми разнообразными, например:

В биполярных транзисторах фликкер-шум вызывается ловушками, связанными с загрязнениями и дефектами кристаллической решетки в переходе между базой и эмиттером.
В полевых транзисторах с управляющим PN-переходом (JFET) он вызывается генерацией носителей в ловушках в обедненном слое канала.
В мОп-транзисторах (MOSFET) главными виновниками шума являются поверхностные дефекты.

Частота, ниже которой интенсивность фликкер-шума начинает превышать интенсивность белого шума, называется частотой излома (FC, рисунок 5). Как правило, частота излома лежит в диапазоне 0,1 Гц…1 кГц и варьируется в зависимости от источников шума.

Фликкер-шумы от различных источников суммируются согласно правилу сложения среднеквадратичных значений. После чего фликкер-шум описывается одним источником, действующим на входе или выходе полупроводникового прибора и характеризующимся одной результирующей плотностью шума и одной частотой излома.

Осциллограмма розового шума выглядит как осциллограмма белого шума с дополнительной низкочастотной компонентой. Пример осциллограммы розового шума приведен на рисунке 7.

Рис. 8. Осциллограмма шума, вызванного случай-
ными скачками тока (0,4 с/дел.)

Шум, вызванный случайными скачками тока (popcorn noise). Шум, вызванный случайными скачками тока (также называемый импульсным шумом, burst noise) — это низкочастотные модуляции тока из-за захвата и эмиссии носителей заряда. Чаще всего такой тип шума встречается в биполярных транзисторах, а его причиной является загрязнение полупроводниковых материалов ионами тяжелых металлов. Свое название он получил из-за «щелчков», производимых им в динамике. Эти щелчки носят случайный характер с частотой ниже 100 Гц и характеризуются дискретной амплитудой и длительностью 1 мс…1 с.

Плотность импульсного шума растет с уменьшением частоты:

Здесь K — константа, определяемая прибором, I — постоянный ток, Fc — частота излома, f — частота.

Шум, вызванный случайными скачками тока, выглядит на осциллограмме как большие, низкочастотные, длительные скачки напряжения. Пример такой осциллограммы приведен на рисунке 8.

Случайные шумы от всех источников суммируются согласно правилу сложения среднеквадратичных величин. После этого они описываются одним источником, действующим на входе или выходе интегральной схемы и характеризующимся одной результирующей плотностью шума и одной частотой излома.

Описание шумовых характеристик в технической документации

Сведения о шумовых параметрах прибора приводятся либо в таблице электрических параметров, либо в разделе типовых условий эксплуатации технического описания. Будьте внимательны: шумовые характеристики приводятся в виде типовых значений и, следовательно, никто не гарантирует, что реальные значения будут именно такими. Шумовые параметры приводятся только для того, чтобы потребитель представлял себе разумный порядок этих величин.

Параметры во временной области

В технической документации данные о шуме обычно приводятся в виде напряжения в определенной полосе частот: как размах шумового напряжения и/или как среднеквадратичное напряжение. В таблице 1 показано, в каком виде приведены данные по шумовому напряжению в технической документации на источник опорного напряжения MAX6129_21.

Таблица 1. Спецификация шума, взятая их технического описания микросхемы опорного напряжения MAX6129_21

Параметр	Обозначение	Условия	Мин.	Тип.	Макс.	Единицы измерения
Динамические характеристики
Напряжение шума	eOUT	f = 0,1…10 Гц	30			µVP-P
		f = 0,01…1 кГц	115			µVRMS

Первое приведенное значение (30 мкВP-P) — это фликкер или 1/f-шум. Определить, что это именно фликкер-шум, можно по заданной в колонке «условия» полосе в низкочастотном диапазоне (0,1…10 Гц). Заметим, что в данном случае приводится размах шумового напряжения (единицы измерения мкВP-P — мкВ (пик-пик)), а не среднеквадратичное значение (измеряется в мкВRMS — мкВ (скв)). Это связано с тем, что шум в указанной полосе наиболее интересен в приложениях, работающих на постоянном токе, где особое внимание уделяется пиковым ошибкам.

Вторая приведенная величина — это среднеквадратичное значение шумового напряжения (единицы измерения в мкВRMS), измеренного в более широкой полосе и на более высоких частотах, где доминирует белый шум, а шум 1/f незначителен. Заметим, что приводится среднеквадратичная величина (а не размах, измеряемый в мкВP-P), поскольку шум, определенный в широкой полосе частот, наиболее интересен в высокочастотных приложениях, в которых необходимо обеспечивать требуемые отношения «сигнал/шум» (SNR). При измерениях величины SNR используется среднеквадратичное значение шума.

Шумовые параметры АЦП и ЦАП очень похожи на шумовые параметры источников опорного напряжения.

Параметры в частотной области

Шум также можно определить его спектральной плотностью (ND) на определенной фиксированной частоте или вблизи нее. В таблице 2 показано, в каком виде приведены данные по плотности шума в документации на источник опорного напряжения MAX6126_21. Поскольку плотность шума всегда изменяется с частотой – ее определяют на фиксированной частоте (spot frequency). Эта фиксированная частота приведена в колонке «условия» таблицы электрических параметров. Для MAX6126 дано значение плотности шума 60 нВ/√Гц на частоте 1 кГц. Часто используются и другие частоты измерений: 10 кГц, 100 кГц и 1 МГц.

Таблица 2. Спецификация шума, взятая их технического описания микросхемы опорного напряжения MAX6126_21

Параметр	Обозначение	Условия	Мин.	Тип.	Макс.	Единицы измерения
Динамические характеристики
Напряжение шума	eOUT	f = 0,1…10 Гц	1,3			µVP-P
		f = 1 кГц, CNR = 0	60			нВ/√Гц
		f = 1 кГц, CNR = 0,1 мкФ	35

Напряжение шума в полосе частот можно оценить, взяв спектральную плотность шума (ND) из таблицы электрических параметров и верхнюю (Fh) и нижнюю (Fl) рабочие частоты:

В данное уравнение не входит фликкер-шум и, следовательно, оно верно только для диапазонов, частота нижней границы которых существенно больше частоты излома (F_l >> F_C). Тем не менее, можно предсказать напряжение шума в любой желаемой полосе частот, если заданы спектральная плотность шума (ND) и частота излома (Fc). Эти данные можно найти в таблице электрических параметров технического описания прибора или определить по графику «зависимость спектральной плотности шума от частоты» в разделе типовых условий эксплуатации. Например, в разделе типовых условий эксплуатации технического описания на источник опорного напряжения MAX6143 приведен график спектральной плотности шума, представленный на рисунке 9.

Рис. 9. График спектральной плотности шума
MAX6143

Рис. 11. График спектральной плотности шума
MAX6143 с линиями ND и 1/f

Оценка амплитудных значений шума, не приведенных в таблице электрических параметров

Если известны спектральная плотность шума (ND) и частота излома (Fc), то напряжение шума в любой полосе частот можно оценить, используя уравнения 1 и 3.

Рис. 10. Схема источника опорного напряжения

Для оценки напряжения шума необходимы четыре исходные величины:

ND — спектральная плотность шума;
FC — частота излома;
Fl — нижняя граница полосы частот;
Fh — верхняя граница полосы частот.

ND и Fc обычно можно найти либо в таблице электрических параметров технического описания, либо определить по графику спектральной плотности шума, приведенному в разделе типовых условий эксплуатации. Возьмем для примера ИОН MAX6143. Оценим фликкер-шум и шумовое напряжение на выходе в полосе звуковых частот (20 Гц…20 кГц). Схема показана на рисунке 10.

Используя выполненный в логарифмическом масштабе график спектральной плотности шума, можно найти Fc на пересечении линий ND и 1/f. На рисунке 11 эти линии выделены красным цветом. В данном случае плотность шума ND = 910 нВ/√Гц, а частота Fc = 0,3 Гц.

Подставим в уравнение 3 следующие значения: ND = 910 нВ/√Гц, F_C = 0,3 Гц, F_l = 0,1 Гц и F_h = 10 Гц. Получаем напряжение шума, равное 3,06 мкВRMS (скв). Перейдя с помощью уравнения 1 к VP-P, найдем, что фликкер-шум = 20,2 мкВP-P (рисунок 12). Этот результат хорошо согласуется с приведенным в документации значением.

Рис. 12. Оценка фликкер-шума для MAX6143

Рис. 13. Оценка напряжения шума на выходе
MAX6143 в полосе звуковых частот

Нахождение напряжения шума, не приведенного в таблице электрических параметров

Уравнения 1 и 3 можно использовать для нахождения шумового напряжения на выходе в любой представляющей интерес полосе частот. Например, можно найти шумовое напряжение на выходе MAX6143 в полосе звуковых частот от F_l = 20 Гц до F_h = 20000 Гц. Используя значения ND = 910 нВ/√Гц, F_C = 0,3 Гц, F_l = 20 Гц и F_h = 20000 Гц, получим, что расчетная величина напряжения шума равна 128 мкВRMS (рисунок 13).

Калькулятор теплового шума

Для быстрого выполнения приведенных выше расчетов шумовых характеристик имеется бесплатный калькулятор. Его можно загрузить по ссылке: http://www.maximintegrated.com/tools/ calculators/hp50g/. Щелкните по ссылке и выберите Thermal Noise Calculator (TNC). В TNC входит «руководство пользователя» (User’s Guide), в котором есть инструкции по использованию калькулятора, приведены уравнения и обоснования и, что наиболее важно, практические примеры использования калькулятора при разработке и анализе схем.

TNC — это программа, написанная для калькулятора HP®* 50g, которая предназначена для анализа теплового шума, исходящего из резисторов и других источников. Этот калькулятор позволяет найти напряжение шума, генерируемого устройством, если известны спектральная плотность белого шума и частота излома 1/f. Каждый параметр может быть задан или найден. TNC может также работать на персональных компьютерах с ОС Windows®** с помощью бесплатной программы HPUserEdit 5.4, которую можно найти на www.hpcalc.org или на странице http://www/maximintegrated.com/tools/ calculators/hp50g/.

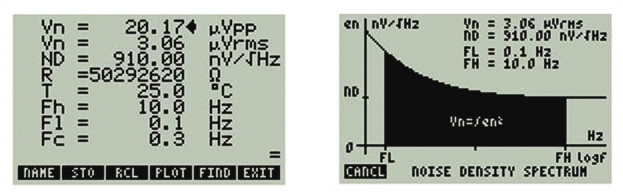
Рис. 14. Вид калькулятора теплового шума

Можно ввести или найти семь параметров, описанных в этой статье (рисунок 14):

напряжение шума (Vn) в мкВP-P (μVP-P) или мкВRMS (μVRMS);
спектральная плотность белого шума (ND) в нВ/√Гц (nV/√Гц);
сопротивление Джонсона (R) в Ом (П);
температура (T) в °C;
верхняя граница частотного диапазона (F_h) в Гц (Hz);
нижняя граница частотного диапазона (F_l) в Гц (Hz);
частота излома (F_C) для 1/f в Гц (Hz).

Заключение

Во всех полупроводниковых приборах есть внутренние источники, генерирующие шум. Все шумы нежелательны, и разработчики должны знать, как можно уменьшить их уровень или, если возможно, вообще их исключить. В этой статье мы обсудили характеристики шумов в полупроводниках и объяснили, в каком виде шумовые параметры приводятся в технической документации на полупроводниковые приборы. Было продемонстрировано, как можно оценить шум источника опорного напряжения в условиях, не приведенных в техническом описании.

Источник